0_Shadow Mapping.md

GAMES202 笔记

渲染方程

$$ L_0(p,w_0) = L_e(p,w_0) + \int_{H^2} f_r(p,w_i\rightarrow w_o) L_i(p,w_i) cos\theta_i dw_i \tag{3.1} $$

实时渲染中的渲染方程通常写为： $$ L_0(p,w_0) = L_e(p,w_0) + \int_{\Omega^+} L_i(p,w_i) f_r(p,w_i,w_o) cos\theta_i V(p,w_i) dw_i \tag{3.2} $$ 这里公式中的 $L_i( p ,w_i)$ 与 $V( p ,w_i)$ 相乘才等同于上一公式的 $L_i( p ,w_i)$，表示将（光源是否存在） 和（光源能否打到 $p$ 点）两项分开考虑

Shadow Mapping

基本思想

这里只考虑点光源或者平行光源。

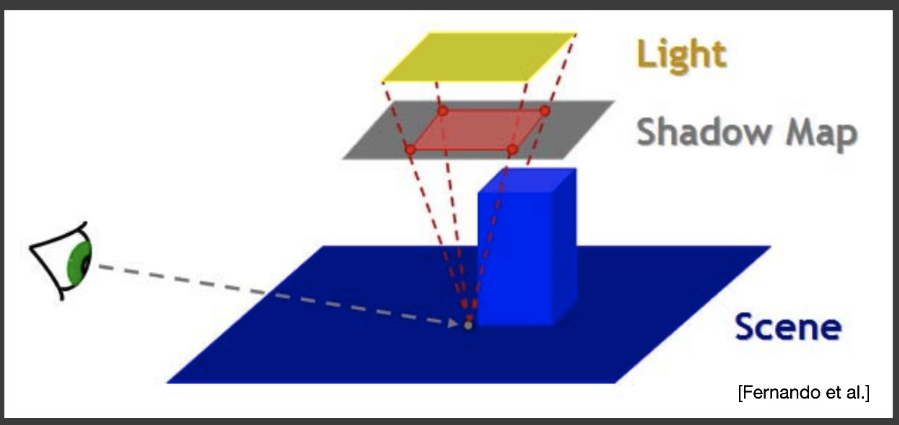
两趟算法：以点光源为例，第一趟，将摄像机放在点光源的位置，渲染出一张shadow map，其实是depth map，用来记录光源看到的最近的点的深度。第二趟，用实际的观察点渲染场景，对摄像机看到的每一个点 $p$ ，通过矩阵变换，将其投影到上一张shadow map中，查询投影坐标上的depth值， 和 $p$ 点到光源的距离做比较，如果depth值（绝对值）<距离，表明有物体挡在了光源和 $p$ 点之间，则 $p$ 点应该显示阴影。

需要注意：shadow map中保存的是世界坐标系下场景中顶点的真实深度（点到光源的真实距离）还是在裁剪空间（视锥体frustum需要经过仿射变换变为正方体形状的裁剪空间）内的z值？进行深度比较时，要保证比较双方的意义是相同的。

平行光源和点光源的区别在于观察空间不同，平行光源是一个长方体，点光源是平截头体。

存在问题

1. Self occlusion（自遮挡）

由于shadow map本身是有分辨率的，所以它每个像素中用一个值表示一片区域的深度值。对地面上的一个点 $p$ ，如果它对应的shadow map中的深度值小于 $p$ 点到光源的距离（真实的深度值），即 z < dis 时，就会被判定为遮挡，尽管真实情况是未被遮挡。

解决方法：我们可以设定一个bias来抵消上面提到的两个距离的差值，当z + bias < dis 时才判定为遮挡。考虑到在 $p$ 点，如果光源是近乎垂直打在地面上的，那儿shadow map中的值和 $p$ 的深度值差异会很小，bias就可以很小。如果光束方向近乎平行于地面（grazing angle），那么该差异可能很大，bias也需要较大。因此可以用入射光的角度$\theta$来控制bias的大小。

但设置bias会带来另一个问题：detached shadow。

2. Detached shadow

设置bias后，有可能出现这种情况，即本来判定为遮挡的点，因为bias的存在，被判定为不遮挡。那么当bias较大时，就会出现上图的状况。

3. Aliasing（走样）

还是由于shadow map的每一个像素代表了一块区域，那么当遮挡物离 $p$ 点较远时，或者场景很大时，一个像素的投影区域就会变得很大，就会出现上图中左边的锯齿现象。

解决方法：cascaded shadow map等

Second Depth Shadow Mapping

(试图解决自遮挡和detached shadow的方法，但因耗费太高而没有人用)

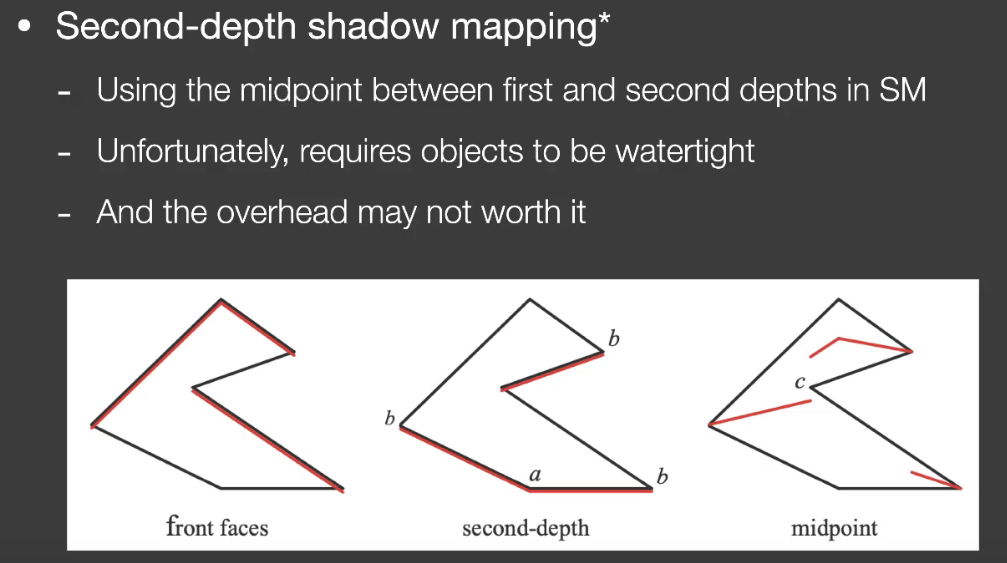
这个方法和最基础的Shadow Mapping方法的区别就是，它采用最小深度和次小深度的均值来作为shadow map中的值。因为不采用bias，所以不会出现detached shadow；如果最小深度和次小深度的值相差较大，也会一定程度减少自遮挡（个人理解）。但缺点就是①：需要模型是一个“盒子”类的东西（watertight）②：保存每个像素的最小深度和次小深度，尽管时间复杂度相同为$O(n)$，但这种方法前面的常数部分更大，耗费要更高。

电子竞技不相信眼泪

PCF（Percentage Closer Filtering）

PCF是抗锯齿，反走样的一种技术。

基本思想：对一个像素的某个属性，取它周围多个像素属性的平均值。

在Shadow Mapping中的应用：可用于实现面光源的软阴影的效果

对于一个点 $p$，它到光源的距离是dis，通过与shadow map中深度值z的比较，我们可以得到它的可见性，从而确定它是否显示阴影。而PCF则是将dis与shadow map上的一块区域的深度值作比较，得到一系列的可见性值（0或1），再求这些可见性的均值。用此值去确定阴影颜色的深浅。

这块filter的区域越大，平均的像素也就越多，可以实现越模糊，越软的阴影。

PCSS（Percentage Closer Soft Shadows）

Percentage-Closer Soft Shadows (nvidia.com)

通过现实中的景象，我们可以观察到阴影在不同位置的软度是不同的。虽然上图有景深导致的模糊，但还是能说明这个问题。

所以需要确定：对于不同位置的着色点 $p$ ，采用多大的filter？

图中 $w_{Penumbra}$ 表示软阴影的范围大小，即软的程度。从上图中可以总结出，影响它的因素有：面光源的大小 $w_{Light}$、面光源到遮挡物的垂直距离 $d_{Blocker}$、面光源到阴影接收物的垂直距离 $d_{Receiver}$。根据相似三角性原理： $$ w_{Penumbra} = (d_{Receiver} - d_{Blocker}) \cdot w_{Light} / d_{Blocker} \tag{3.4} $$ 实际应用时，如下图（个人理解）：

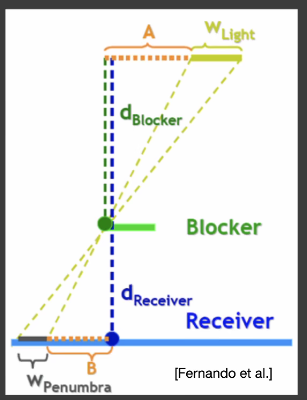
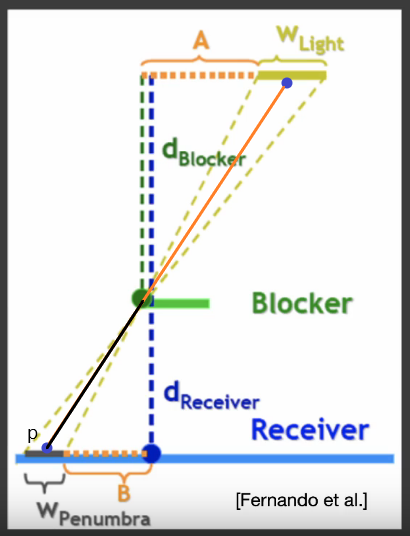
将面光源水平放置，（假设接收物和面光源平行就好，不影响p点接收到的光）。那么公式里的 $d_{Blocker}$ 就是橙色的那一段，$d_{Receiver}$ 就是橙色 + 黑色的那一段。

假设 $w_{Light}$ 已知，着色点 $p$ 到光源的距离 $d_{Receiver}$ 也可求。而 $d_{Blocker}$ 就是shadow map中记录的深度值（因为面光源无法生成shadow map，所以应该将面光源看作点光源，生成一张shadow map，比如用面光源中心的点）。

因为是面光源，所以对于我们要着色的一个点 $p$，遮挡物上不同的位置都可能挡住了一些入射光，所以需要求一个平均的 $d_{Blocker}$，就是对shadow map上的一个区域中的 $d_{Blocker}$ 求平均值（需要注意，如果shaodow map中的点没有遮挡住 $p$，那就不算遮挡物，不参与平均值计算），那么又有了一个问题，这个区域的大小应该取多少？

有一个方法是，让点 $p$ 连向光源的四个顶点（假设是四个），看这个视锥在shadow map上覆盖了多大的区域，用这个区域来当作求均值的区域。这种方法是很符合直观想象的，我们想求的就是遮住点 $p$ 的blocker的范围，从图中看自然就是红色的区域。

至此，就可以完成整个流程：

1. （Blocker search）让点 $p$ 连向面光源的四个顶点，看这个视锥在shadow map上覆盖了多大的区域，在这个区域中计算平均 $d_{Blocker}$。

2. （Penumbra estimation）用公式(3.4) 计算软阴影范围大小，确定PCF的滤波范围。

3. （Percentage Closer Filting）使用PCF，求出点 $p$ 的阴影深浅程度。

VSSM（Variance Soft Shadow Mapping）

上述过程中，第1步和第3步中，对shadow map中每个像素，需要对它的一个邻域进行某个属性的加权平均，要访问邻域内每个像素的值，那么这种操作的时间耗费就会很高。而VSSM没有访问每一个像素值，而是用一种巧妙的方法得到我们所需要的值。

简化PCF

对于第三步的PCF，我们的操作是，对一个点 $p$，将它到光源的距离dis和shadow map上一块区域内的深度值比较，得到一系列的可见性值（0或1），将这些值平均，得到最终的可见性值。看起来我们需要知道邻域内每个像素的值，但实际上我们只需要知道邻域内有百分之多少的深度值是大于dis的就可以了。于是VSSM在这里使用了一个近似，即切比雪夫不等式：

如果随机变量 $X$ 满足一个均值为 $\mu$，方差为 $\sigma$ 的概率分布，对于某一个 $t$ （$t>\mu$ ）则有： $$ P(x>t) \leq \frac{\sigma^2}{\sigma^2 + (t-\mu)^2} $$ （一位知乎答主对切比雪夫不等式的解释：https://www.zhihu.com/question/27821324/answer/80814695

带入到PCF中，意义为，对于一个点，它到光源的距离为 $t$，我们希望得到这个点对应shadow map的邻域中深度值大于 $t$ 的概率 $P$。由切比雪夫不等式我们知道，$P$是小于不等式右边的值的，但VSSM采用了一个大胆的假设：把不等式变为等式，将不等式右边的值赋给 $P$。这样我们只需要知道这个邻域中深度值的均值和方差就可以完成PCF。

假设均值已知，那么方差可用高数课本里的公式求出：$Var(X) = E(x^2) - E^2(X)$。我们现在只需要知道该邻域的深度值均值，以及深度值平方的均值。

这里的邻域为矩形区域，求一个矩形区域的均值，leetcode上刷的题终于有了用武之地。

前缀和！

这里不再细说了。均值可用前缀和算法求得，对于平方的均值，可以维护一个深度值的平方的map，同样用前缀和得到均值。

简化Blocker search

虽然这一步也是求一块区域内的深度值均值，但却有一点需要注意，这里求的是矩形区域内blocker的深度值均值，而不是所有深度值的均值。

即在上图的矩形区域中，假设着色点的深度值是7，那么只需要求蓝色数字的均值。来看这样一个公式： $$ \frac{N_1}{N}z_{unocc} + \frac{N_2}{N}z_{occ} = z_{avg} $$

$N$为矩形区域的像素数，$z_{avg}$为矩形区域内的平均深度；$N_1$为非遮挡物所占的像素数，$z_{unocc}$为非遮挡物的平均深度；$N_2$为遮挡物所占的像素数，$z_{occ}$为遮挡物的平均深度。显然等式成立。

我们想要求得$z_{occ}$，而$\frac{N_1}{N}$可用上面小节提到的切比雪夫不等式近似求得，$\frac{N_2}{N} = 1 - \frac{N_1}{N}$，那么只需要知道$z_{unocc}$就可以了。这里VSSM又做了一个更大胆的假设：认为非遮挡物的深度和当前着色点的深度相同（依据是绝大多数阴影的接收物是个平面），即认为$z_{unocc}=7$，那么除$z_{occ}$的所有变量都是已知的，$z_{occ}$可求。

虽然VSSM耗费大大降低，但目前基本不用这种方法，因为图像降噪的技术非常成熟，可以在采样的PCSS中进行降噪，来达到很好的效果。

存在问题

切比雪夫不等式 $$ P(x>t) \leq \frac{\sigma^2}{\sigma^2 + (t-\mu)^2} $$ 由于我们由于我们是把切比雪夫不等式当成了等式来使用，那么我们得到的 $P$，是比真实的 $P$ 大的。而 $P$ 表示百分之多少的深度值是大于dis的（没有挡住点 $p$ ），就是说这个值越大，得到的可见性值越大，点 $p$ 越亮。即最终得到的图像比实际场景要亮。当这个误差很大时，就会出现漏光问题（Light Leaking）：

MSM（Moment Shadow Mapping）

在VSSM里，切比雪夫不等式来近似求得一个概率，也就是CDF，但这个CDF是不精准的。因此如果能够找到更精确的CDF，就可以得到更精准的结果。

数学概念：矩（moment）是对变量分布和形态特点的一组度量。n阶矩被定义为一变量的n次方与其概率密度函数（PDF）之积的积分。

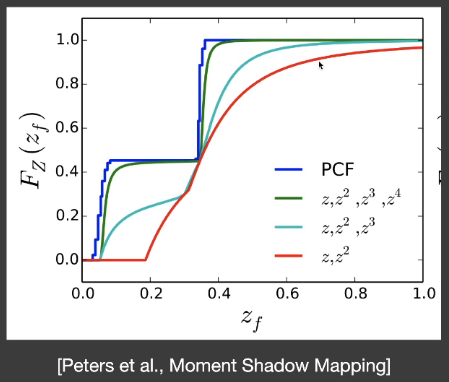
VSSM中只用到了 $X$ 和 $X^2$,，可以认为只用到了前两阶矩，如果再考虑到更高阶的矩，就可以重建一个更加准确的CDF。

图中PCF是书写错误，应该为CDF。可以看到使用前四阶矩得到的CDF就非常精准了。

那么如何用矩得到这样一个CDF，还得看论文：https://jankautz.com/publications/VSSM_PG2010.pdf

这一步的耗费也是很高的。

Distance Field Soft Shadows

signed distance function（符号距离函数）

signed distance function（符号距离函数）：对空间中的任意一点，它到一个物体表面有一个最小距离（根据在物体的内外可能区分正负）。

对一个点，它到这个场景的最小距离就是它到每一个物体的最小距离的最小值。空间中每一个点都有这样一个最小距离，这些距离在空间中形成了一个标量场。

应用：

1. 对移动边界的位置进行插值（对每一个点到黑白边界线的distance function进行插值）。

   

2. 融合两个物体（具体方法：对两个distance function进行插值？？不确定）

   

SDF在阴影中的应用

阴影，可以理解为在着色点 $p$ 处，面光源被遮挡的越多就越暗。SDF可以得到一个着色点被遮挡的程度，也就得到了visibility。

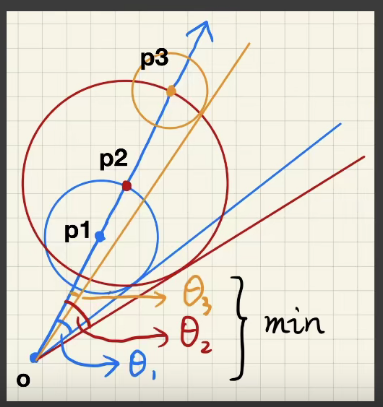
对图中圆圈中的点，圆的半径表示它的SDF的值，意味着在以此点为圆心，此半径为球的内部，是没有任何物体的；也就是说在这个球内，没有物体会遮挡住下方的着色点。

和Ray-marching结合，我们可以粗略的估计出着色点被遮挡的程度。如上图，假设从o点射向光源的ray，在点 $p_1$ ，我们查询SDF得到一个半径，可以求得角度 ${\theta}_1$，粗略的认为 ${\theta}_1$内的方向角内没有物体遮挡住光源。然后在ray方向上找到点 $p_2$ 。重复此过程，直至ray走了足够远的距离或者ray与一个物体相交。取各个 $\theta$ 的最小值，就得到了未被遮挡的范围大小。

勾股定理求出 $\theta$ : $$ {\theta} = arcsin\frac{SDF(p)}{||p-o||} $$ 而实际应用中，反三角函数运算量很大，因此可以转化为： $$ {\theta} = min{\frac{k\cdot SDF(p)}{||p-o||}, 1.0} $$ 用k来调整软阴影的大小。k越大，意味着足够小的 $\theta$ 就可以使visibility达到1.0，阴影就越硬，反之则越软。

Pros & Cons：

Pros：速度快，质量高

Cons：空间中每个点的SDF需要预计算，存储空间耗费也很高。